Calculus

Click here to return to the gallery.

Volume under a surface comprised of Riemann boxes.

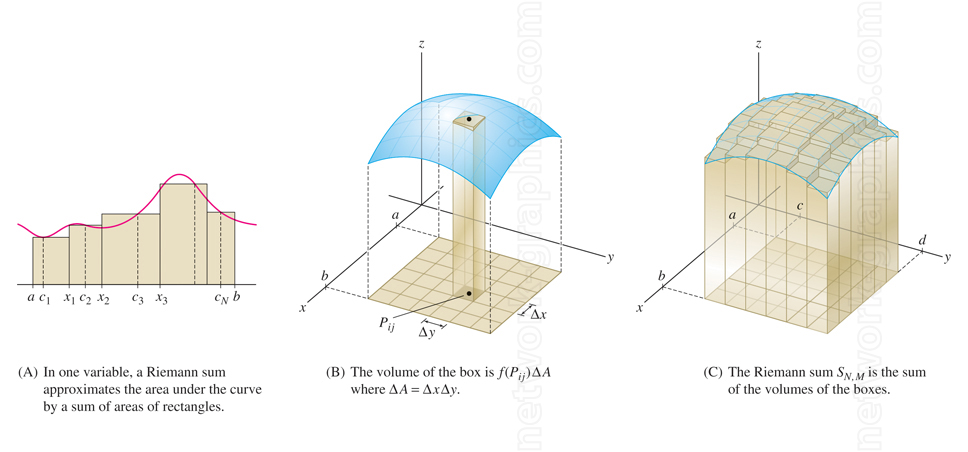
Illustration of Riemann sums, showing area under a curve with rectangles in one dimension, and in two dimensions with small boxes beneath a 3D surface to approximate total volume.

This illustration demonstrates the concept of Riemann sums in both one and two variables to approximate areas and volumes under curves and surfaces. In part (A), the classic one-dimensional Riemann sum approximates the area under a curve by summing rectangular slices. Part (B) extends the idea to two dimensions, where a small box at the surface height f(pij) over an area element ΔA = Δx Δy contributes to the total volume. Part (C) illustrates a Riemann sum approximation for the total volume under a surface by summing the individual box volumes.

This illustration is ideal for use in textbooks on calculus, engineering mathematics, and physics, enhancing comprehension of how integration sums up infinitesimal contributions over an interval or surface.

We can provide sample images or create custom illustrations tailored to your projects. If you are looking for an illustration of this type, or from another subject area, you can contact us to discuss your needs.

Network Graphics / Division of Abramson & Wickham Graphics Inc.
All rights reserved.